S₂ - Площадь закрашенной части фигуры вычисляется по формуле:
S(всей фигуры)-S₁(незакрашенной части фигуры)=S₂
Например:
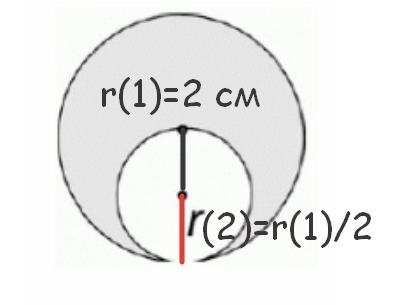
Дана фигура: в больший круг с радиусом r₁, вписан меньший круг так, что радиус большего круга является диаметром меньшего, и равен 2 см.
Больштй круг закрасили, оставив меньший круг незакращенным.
Найти площадь закрашенной части большего круга.
1. Площадь большего круга: S=πr²
2.Если диаметр малого круга равен радиусу большего круга, то радиус меньшего круга: r₂ = r₁/2, площадь меньшего круга: S₁=π(r/2)²
3. Площадь закрашеной части фигуры: S₂=πr²-π(r/2)². Примем: π=3.14
S₂=3.14*2²-3.14*(2/2)²=
3.14(4-1)=3.14*3=9.42
S₂=9.42 см²
Ответ: Площадь закрашенной части фигуры равна 9.42 см²
Проверка: S=3.14*2²=12.56 см²
S₁=3.14*1=3.14 см²
S₂=12.56-3.14=9.42 см²
Рисунок во вложении