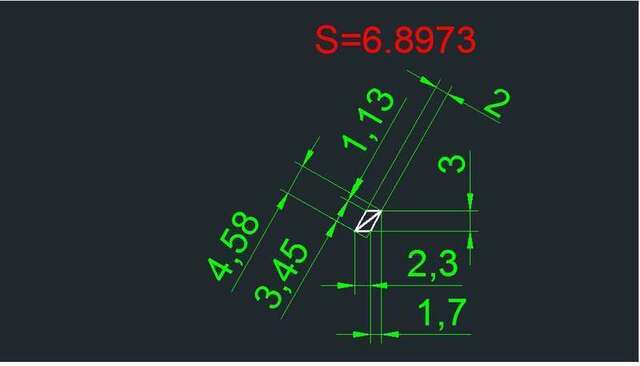
Диагональ с двумя высотами образует 2 треугольника.
Обозначим углы против этих высот за α и β.
Тогда sin α = 3/5. а sin β = 2/5.
cos α = √(1-9/25) = 4/5
cos β = √(1-4/25) =√21/5.
Острый угол параллелограмма равен сумме α и β.
Для определения площади параллелограмма надо найти его основание, которое равно 5*cos α - 3 / tg(α+β).
tg(α+β) = (tg α+tg β) / (1 - tg α*tg β).
tg α = sin α / (1-sin²α) = (3/5) / (√(1-9/25)) = 3 / 4,
tg β = (2/5) / (√(1-4/25)) = 2 / √21.
tg(α+β) = ((3/4)+(2/√21)) / (1-(3/4)+(2/√21)) = 1,76376.
Основание равно 5*(4/5) - 3/1,76376 = 2,29909.
Площадь параллелограмма равна: 3*2,29909 = 6,89727.