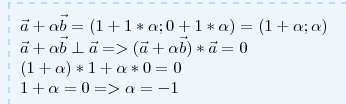Даны вектора а=(1; 0) и b=(1; 1).найдите альфа, чтобы вектора а+альфа*b и а были...

Question

Даны вектора а=(1; 0) и b=(1; 1).найдите альфа, чтобы вектора а+альфа*b и а были перпендикулярными.помогите?!

Answer 1

Так как векторы перпендикулярны, то скалярное произведение равно 0:
1+α=0  ⇒  α= - 1

Answer 2

(\vec a+ \alpha \vec b)*\vec a=0 \\ (1+ \alpha )*1+ \alpha *0=0 \\1+ \alpha =0=> \alpha =-1 " alt="\vec a+ \alpha \vec b=(1+1* \alpha ;0+1* \alpha )=(1+ \alpha ; \alpha ) \\ \vec a+ \alpha \vec b \perp \vec a=>(\vec a+ \alpha \vec b)*\vec a=0 \\ (1+ \alpha )*1+ \alpha *0=0 \\1+ \alpha =0=> \alpha =-1 " align="absmiddle" class="latex-formula">

Ответ: -1

---