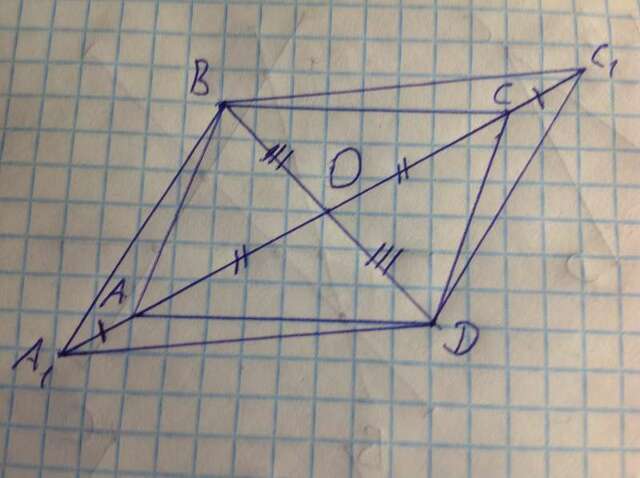
Проведём диагональ BD. В параллелограмме ABCD диагонали делятся пополам точкой О их пересечения. Тогда AO=CO. Кроме того, известно, что AA1=CC1. Тогда A1O=A1A+AO=C1C+CO=C1O. Таким образом, в четырехугольнике A1BC1D диагонали в точке пересечения также делятся пополам. Рассмотрим треугольники BOC1 и A1OD, они равны по двум сторонам и углу между ними (углы BOC1 и A1OD равны как вертикальные). Тогда BC1=A1D. Аналогично, рассмотрим треугольники A1OB и C1OD, которые также равны по двум сторонам и углу между ними, тогда A1B=C1D. Таким образом, в четырехугольнике A1BC1D противоположные стороны попарно равны, тогда это параллелограмм. В параллелограмме противоположные углы равны, тогда BA1D=BC1D, что и требовалось доказать.