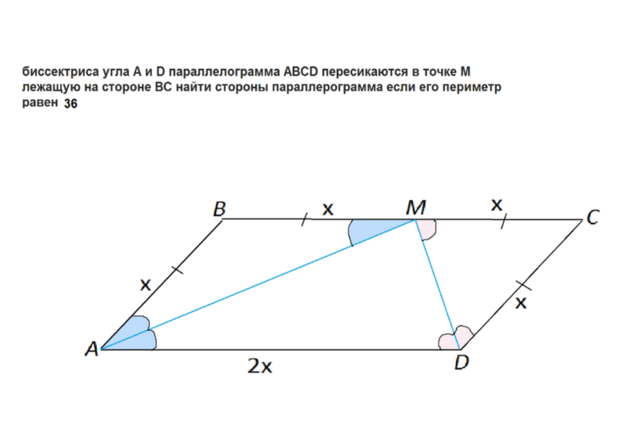
Биссектриса угла параллелограмма отсекает от него ( от параллелограмма)
равнобедренный треугольник.
В самом деле, угол ВМА=углу МАD как накрестлежащие при пересечении параллельных прямых секущей ( а стороны параллелограмма параллельны, на то он и параллелограмм).
А угол ВАМ=∠ МАD.
Отсюда∠ВАМ=
∠ВМА, и треугольник АВМ - равнобедренный.
На том же основании треугольник СМD также равнобедренный.
Но АВ=СD.
Следовательно, ВС=2 АВ=АD
АВ+ВС+СD+АD=6 АВ
6АВ=36
АВ=
СD=
6
ВС=
АD=
12