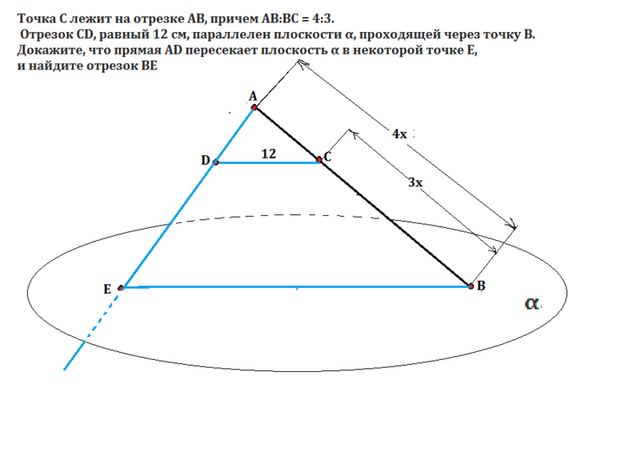
Имеем 3 точки, две из которых лежат на отрезке, а одна не лежит на нем.
Это точки А, В, D.
Через три точки пространства, не лежащие на одной прямой, можно провести плоскость, притом только одну. (Аксиома).
Точки А, В, С, D лежат в одной плоскости.
Значит, и точка Е, как лежащая на прямой АD, лежит в этой плоскости.
Точки В и Е принадлежат обеим плоскостям, значит, эти плоскости пересекаются по прямой ВЕ.
Прямая ВЕ - линия пересечения плоскости α и плоскости ЕАВ, СD || плоскости α по условию.
Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения этих плоскостей. ⇒
CD || ВЕ, отрезки АЕ и АВ секущие при этих параллельных прямых.
По свойству углов при параллельных прямых и секущей
в треугольниках АDС и АВЕ ∠АСD =∠ АВЕ и ∠АDС=∠АЕВ как соответственные, угол А - общий. ⇒
∆ АDС ~∆ АВЕ по первому признаку подобия треугольников. .
Из подобия треугольников следует:
ВЕ:СD=АВ:АС
Пусть коэффициент отношения АВ и ВС равен х.
Т.к. АВ:СВ=4:3, то
АС=4х-3х=1х
ВЕ:12=4:1 ⇒
ВЕ=48 см