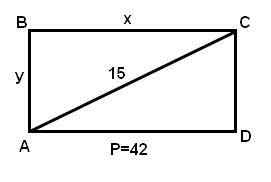
5. Периметр прямоугольника - P=2(a+b). Подставим в формулу известные значения:
2(x+y)=42(:2)
x+y=21 - это одно из уравнений в системе уравнений. В принципе полученное уравнение присутствует только в варианте под буквой "в", но найдем и второе уравнение.
Диагональ делит прямоугольник на два равных прямоугольных треугольника (рисунок вложен ниже). Диагональ - гипотинуза. По пифагору c^2=a^2+b^2. Подставим в формулу известные значения:
x^2+y^2=15^2
x^2+y^2=225
Получаем систему из двух уравнений:
x^2+y^2=225
x+y=21
Ответ: в)
6. Воспользуемся подстановкой. В координате x - первое число, y - второе число.
1) соответствует б):
(7;4)
x^2+2y^2=81
7^2+2*4^2=81
49+2*16=81
49+32=81
81=81;
x^2-2y^2=17
49-32=17
17=17
т.к x и y в обоих уравнениях в квадрате, то координаты (7;-4), (-7;4), (-7;-4) подставлять бессмысленно, т.к x и y в любом случае положительные.
2) соответствует а)
(-5;-3)
xy=15
-5*(-3)=15
15=15;
x+y=-8
-5+(-3)=-8
-8=-8
3) соответствует в)
(5;-1)
x-y=6
5-(-1)=6
6=6;
x^2-y^2=24
5^2-(-1)^2=24
25-1=24
24=24
Ответ: 1-б; 2-а; 3-в