y=0 \\ y=0=>-(x^2-4x)=0 \\ x(x-4)=0 \\ x_1=0;x_2=4" alt="y= \frac{x-4}{4-x}( x^{2} -4x) \\ ODZ:x \neq 4 \\ y= \frac{-(4-x)}{4-x}( x^{2} -4x)=-( x^{2} -4x) \\ x=0=>y=0 \\ y=0=>-(x^2-4x)=0 \\ x(x-4)=0 \\ x_1=0;x_2=4" align="absmiddle" class="latex-formula">
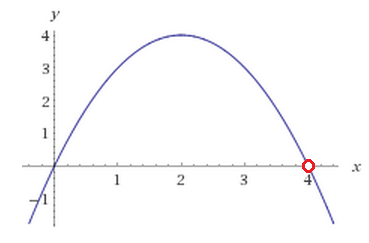
Это график параболы, у которой ветки направлены вниз, пересекает ось х в точках (0;0) и (4;0) (которую потом выколем), а ось у в точке (0;0) - начало координат.
+ Выколотая точка (4;0) по ОДЗ (не удовлетворяет нашему изначальному графику) на графике
Вершина параболы в точке х=-b/2a=4/2=2, координата у=-4+4*2=4 - точка (2;4)