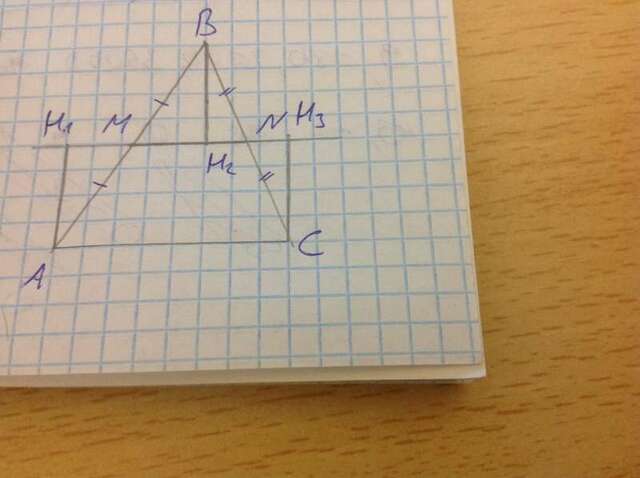
Пусть в треугольнике ABC проведена средняя линия MN (см. рисунок). AH1, BH2, CH3 - перпендикуляры, опущенные из вершин на прямую, содержащую MN, они равны расстояниям от вершин треугольника до этой прямой. Докажем, что они равны.
Рассмотрим прямоугольные треугольники AMH1, BMH2. В них острые углы AMH1 и BMH2 равны, также равны гипотенузы AM и BM, тогда эти прямоугольные треугольники равны по гипотенузе и острому углу. Значит, катеты, лежащие против равных углов в этих треугольниках, равны, то есть, AH1=BH2.
Аналогично, в прямоугольных треугольниках BNH2 и CNH3 BN=CN, а острые углы BNH2 и CNH3 равны как вертикальные. Тогда треугольники равны по гипотенузе и острому углу. Значит, BH2=CH3.
Таким образом, AH1=BH2=CH3, то есть, расстояния от вершин треугольника до прямой, содержащей MN, равны.