В прямоугольнике ABCD AD=28, диагональ AC=35, а биссектриса угла D пересекает ВС в точке...

Question

В прямоугольнике ABCD AD=28, диагональ AC=35, а биссектриса угла D пересекает ВС в точке М, а диагональ в АС в точке К. Найдите длины отрезков МК и КD

Comments

Очень интересная задача :) Когда будете списывать, вникайте :)

---

хорошо, спасибо большое, не могли бы помочь решить? Потому что у меня с математикой туго

Answer 1

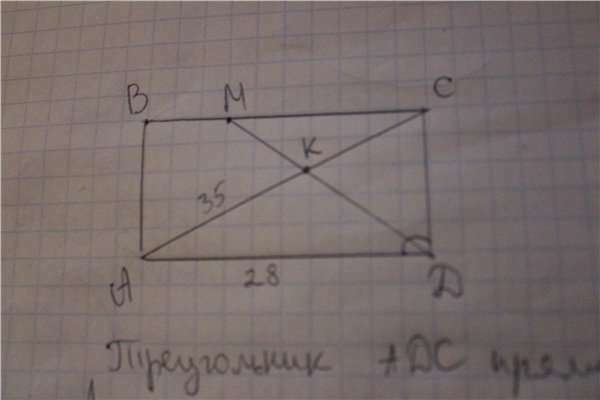
Треугольник  ADС прямоугольный, АС -гипотенуза, АС=35 см;
АD-противолежащий катет, AD=28cм;
СD- прилежащий катет.
Найти МК и КD.
Решение:
AD=AC×sinD
28=35x
x=28÷35
x=0,8.
cos(D)=CD÷AC
0,8=x÷35
x=0,8×35
x=28°
угол D=28°.
Так как MD биссектриса, то она делит угол пополам на равные части.
Значит, угол ADK=14° и угол CDK=14°.
Найдем сторону СD:
AC=CD÷cos(D)
CD=AC×cos(D)
CD=35×0,8=28 см.
Получается, что прямоугольник оказался квадратом, так как стороны равны.
В квадрате равны диагонали, и они пересекаются под прямым углом.
Так как MD=MK+KD, MD=AC=35см, то:
MK=35÷2=17,5 см
KD=35÷2=17,5 cм.
Ответ: MK=17,5 см ; MD=17,5 см.

---