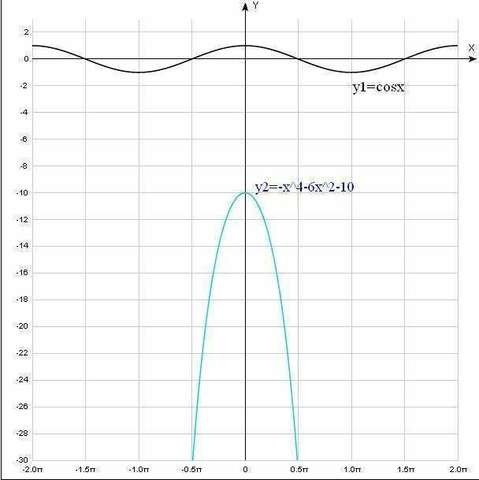
Решим графически:
Решим графически:


Функция косинуса - известная функция.
Для построения функции

:
1) Нули функции:


- график не пересекает ось Ох.
2)

3) Точки максимума и минимума:


- при переходе через эту точку производная меняет свой знак с плюса на минус, значит это точка максимума
4) Функция возрастает при x<0, убывает при x>0.
По рисунку видно, что график функции

всегда ВЫШЕ графика функции

.
Ответ: х - любое число (x∈R)