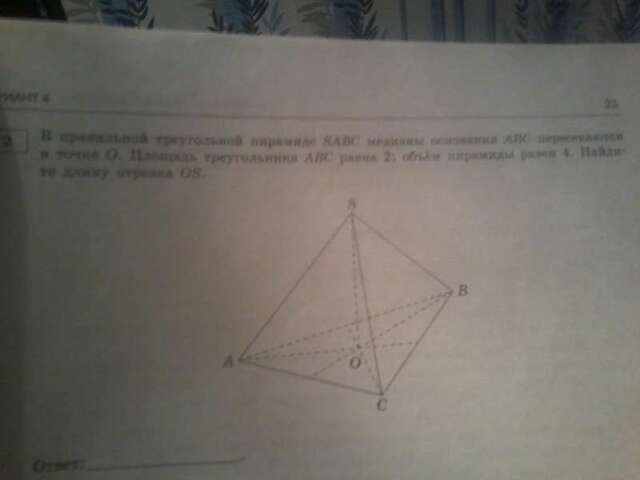
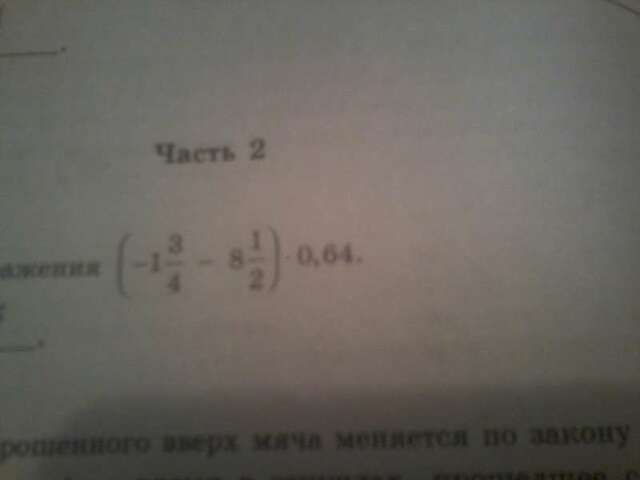Помогите решить задачки ( с полным решением ) 1. Ковбой Джон попадает в муху ** стене с...

Question

30 просмотров

Помогите решить задачки ( с полным решением )

1. Ковбой Джон попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,3. На столе лежат 10 револьверов, из них только 3 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

2. Теплоход проходит по течению реки до пункта назначения 375 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода, если в неподвижной воде равна 20 км/ч, стоянка длится 10 ч, а в пункт отправления теплоход возвращается через 50 ч после отплытия из него.

Математика Killomi_zn (190 баллов) 28 Март, 18 | 30 просмотров

Дан 1 ответ

Akatava_zn · Answer 1 · 2018-03-28T06:49:00+0000

3. $(-1 \frac{3}{4}-8 \frac{2}{4})*0.64=(- \frac{7}{4}- \frac{17}{2})* \frac{64}{100}=( \frac{-7-34}{4})* \frac{64}{100}= -\frac{41}{4}*\frac{64}{100}=\\= \frac{-41*16}{100}=- \frac{656}{100}=-6.56.$

4. OS=h-высота пирамиды.
В основании правильной треугольной пирамиды - правильный треугольник. Формула площади правильного треугольника со стороной а выглядит так:
$S= \frac{ \sqrt{3} }{4}a^2;$ .
Формула объема правильной треугольной пирамиды выглядит так:
$V= \frac{ha^2}{4\sqrt{3}};$
По условию, знаем, что S основания=2, объем=4. Получим:
$\left \{ {{ \frac{ha^2}{4\sqrt{3}}=4; } \atop { \frac{\sqrt{3}a^2}{4} =2;}} \right. \\ \left \{ {{h= \frac{16\sqrt{3}}{a^2}; } \atop {a^2= \frac{8}{\sqrt{3}}; }} \right.\\ h= \frac{16\sqrt{3}}{1}* \frac{\sqrt{3}}{8}=2*3=6. \\OS=6.$