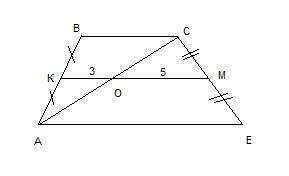
Рассмотрим треугольник АСЕ. Здесь ОМ - средняя линия. Она средняя линия, т.к. соединяет середины сторон треугольника АСЕ. СМ=ЕМ по условию. СО=АО по теореме Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. В нашем случае на прямой СЕ отложено 2 таких равных отрезка: СМ и МЕ. Через их концы проведены параллельные прямые МО и ЕА. MO II EA, т.к. КМ - средняя линия трапеции, параллельная ее основанию АЕ. Параллельные прямые МО и ЕА пересекли вторую прямую АС и отсекли на ней равные между собой отрезки СО и АО.
Средняя линия треугольника ОМ параллельна стороне АЕ и равна ее половине:
ОМ =1/2АЕ, АЕ=2*ОМ=2*5=10 см
Рассмотрим треугольник ВАС. Здесь КО - средняя линия, параллельная его стороне ВС и равная ее половине:
КО=1/2ВС, ВС=2*КО=2*3=6 см