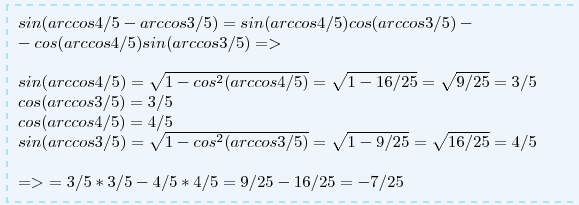\\ \\
sin(arccos 4/5)= \sqrt{1-cos^2(arccos 4/5)}= \sqrt{1-16/25}= \sqrt{9/25}=3/5
\\
cos(arccos 3/5)=3/5
\\
cos(arccos 4/5)= 4/5
\\
sin(arccos 3/5)= \sqrt{1-cos^2(arccos 3/5)}= \sqrt{1-9/25}= \sqrt{16/25}=4/5
\\ \\
=> \ = 3/5*3/5-4/5*4/5=9/25-16/25=-7/25" alt="sin(arccos 4/5-arccos 3/5)=sin(arccos 4/5)cos(arccos 3/5)- \\ -cos(arccos 4/5)sin(arccos 3/5)= >\\ \\
sin(arccos 4/5)= \sqrt{1-cos^2(arccos 4/5)}= \sqrt{1-16/25}= \sqrt{9/25}=3/5
\\
cos(arccos 3/5)=3/5
\\
cos(arccos 4/5)= 4/5
\\
sin(arccos 3/5)= \sqrt{1-cos^2(arccos 3/5)}= \sqrt{1-9/25}= \sqrt{16/25}=4/5
\\ \\
=> \ = 3/5*3/5-4/5*4/5=9/25-16/25=-7/25" align="absmiddle" class="latex-formula">