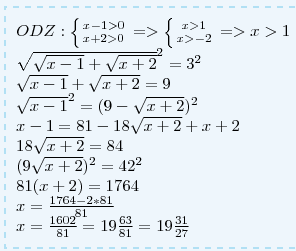0} \atop {x+2>0}} \right. => \left \{ {{x>1} \atop {x>-2}} \right. =>x>1 \\ \sqrt{ \sqrt{x-1} + \sqrt{x+2} }^2=3^2 \\ \sqrt{x-1} + \sqrt{x+2} =9 \\ \sqrt{x-1}^2=(9-\sqrt{x+2})^2 \\ x-1=81-18\sqrt{x+2}+x+2 \\ 18\sqrt{x+2}=84 \\ (9\sqrt{x+2})^2=42^2 \\ 81(x+2)=1764 \\ x= \frac{1764-2*81}{81} \\ x= \frac{1602}{81}= 19 \frac{63}{81}=19 \frac{31}{27} " alt="ODZ: \left \{ {{x-1>0} \atop {x+2>0}} \right. => \left \{ {{x>1} \atop {x>-2}} \right. =>x>1 \\ \sqrt{ \sqrt{x-1} + \sqrt{x+2} }^2=3^2 \\ \sqrt{x-1} + \sqrt{x+2} =9 \\ \sqrt{x-1}^2=(9-\sqrt{x+2})^2 \\ x-1=81-18\sqrt{x+2}+x+2 \\ 18\sqrt{x+2}=84 \\ (9\sqrt{x+2})^2=42^2 \\ 81(x+2)=1764 \\ x= \frac{1764-2*81}{81} \\ x= \frac{1602}{81}= 19 \frac{63}{81}=19 \frac{31}{27} " align="absmiddle" class="latex-formula">