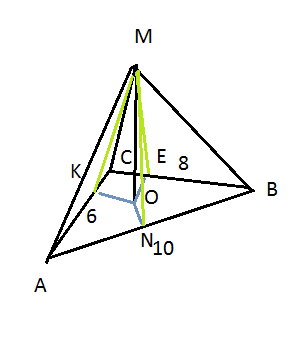
Чтобы получить двугранные углы Надо провести перпендикуляры к сторонам треугольника. Так как все двугранные углы равны, значит Апофемы боковых граней имеют равные проекции, это возможно, в том случае, если О- центр вписанной окружности
По теореме Пифагора
АВ²=АС²+BC²=6²+8²=36+64=100
AB=10
r=(a+b-c)/2=(6+8-10)/2=2
В прямоугольном треугольнике МОК угол КМО равен 30°. Против угла в 30° катет равен половине гипотенузы, значит. МК=4 см
И апофемы двух лругих граней тоже равны 4 см
S(полн)=S(бок)+S(осн)= кв. ед.
кв. ед.