1) (См .рисунок 1) Поскольку плоскость, секущая плоскость рисунка
(плоскость треугольника АВС) в заданных точках (и, естественно, по прямой А1С1)
параллельна прямой АС, то и прямая А1С1 будет параллельна АС. Следовательно,
треугольники АВС и А1ВС1 подобны. Т.к. АВ/АА1 = 10/3, то А1В = АВ – АА1 = 10 – 3 = 7 единиц. Из подобия
треугольником можно записать АС:А1С1 = АВ:А1В = 10:7. Отсюда А1С1 = АС : (10:7)
= АС*7/10 = 15*7/10 = 10,5
см.
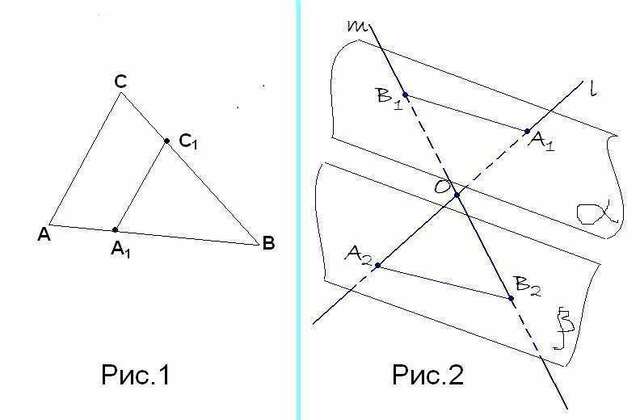
2) (См. рис.2.) Так как
прямые m и l
пересекаются в точке О, то эти прямые задают плоскость, которая пересекает
заданные в задаче плоскости альфа и бета. Т.к. по условию заданные плоскости
параллельны, то и линии пересечения заданных плоскостей с плоскостью,
задаваемой пересекающимися прямыми, будут параллельны. Т.е. А1В1 параллельна
А2В2. Образовавшиеся треугольники А1В1О и А2В2О – подобны, т.к. их углы при
вершинах О равны, т.к. являются вертикальными. И <ОА1В1 = <ОА2В2, как
внутренние накрест лежащие при параллельных прямых. Таким образом, было
показано, что треугольники подобны, поскольку три угла одного треугольника
соответственно равны трем углам другого треугольника. Поскольку В1В2/В1О = 7/3, то В2О будет равно
В1В2 –В1О = 7 – 3 = 4 единицы. Таким образом, В1О/В2О = 3:4. Но поскольку
треугольники подобные, то А1В1/А2В2 = В1О/В2О = 3:4. Отсюда А2В2 = А1В1*4/3 =
9*4/3 = 12 см</p>
3) С построением проекции не понятно. Можно построить
проекцию заданного треугольника на заданную плоскость. А в этой задаче не
задано ни того ни другого.