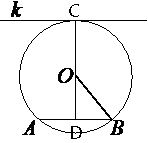Проведем отрезок OB как показано на рисунке.Расстояние от хорды AB до параллельной ей касательной k обозначено как CD.CD=OC+OD, OC - это радиус окружности, найдем OD.По условию задачи k||AB. CD перпендикулярен k (по свойству касательной), тогда CD перпендикулярен и AB (т.к. CD - секущая для параллельных прямых, и внутренние накрест-лежащие углы равны), значит треугольник OBD прямоугольный.
DB=AB/2=102/2=51 (по второму свойству хорды)
OB равен радиусу окружности.
Тогда по теореме Пифагора:
OB(в квадрате)=OD(в квадрате)+DB(в квадрате)
85(в квадрате)=OD(в квадрате)+51(в квадрате)
7225=OD(в квадрате)+2601
OD(в квадрате)=7225-2601=4624
OD=68CD=OC+OD=85+68=153