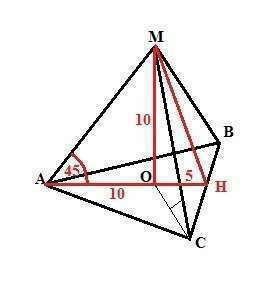
Раз точка М проецируется в центр правильного треугольника, Пирамида МАВС правильная и ее ребра наклонены к плоскости основания под одинаковым углом 45°.
Прямоугольный треугольник МОС - равнобедренный, так как острый угол МСО равен 45° (дано). Следовательно, катеты равны и ОС=МО=10.
Заметим, что АО=ВО=СО=10.
В правильном треугольнике АВС СО=АО - это 2/3 его высоты, а ОН (расстояние от центра О до стороны ВС равно 1/3 его высоты (так как высота = медиана и точкой О делится в отношении 2:1, считая от вершины. Значит ОН=ОС:2=5. В прямоугольном треугольнике МОН, где гипотенуза МН - искомое расстояние, по Пифагору найдем МН=√(МО²+ОН²) или МН=√(100+25) = 5√5.
Ответ: МН=5√5.