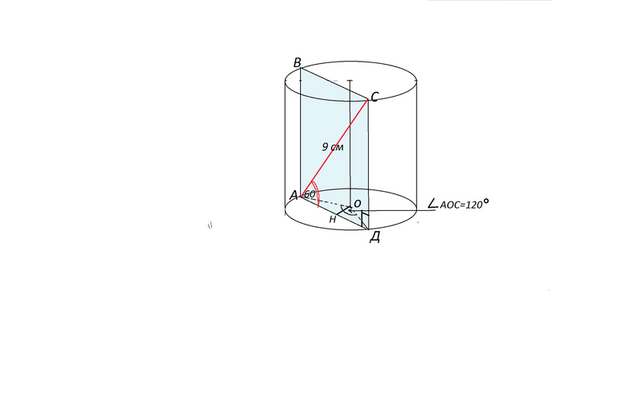
Сделаем рисунок.
Применены формулы высоты правильного треугольника (h=a √3):2,
длины окружности (C=2пR)
площади круга S=пR²,
площади боковой поверхности цилиндра S=2s оснований+ Sбоковая.
---------------------------------
Площадь полной поверхности цилиндра равна сумме площадей двух оснований и площади боковой поверхности.
Для того, чтобы найти их, нужно найти
радиус окружности основания и
высоту цилиндра.
Высоту цилиндра
СД найдем из прямоугольного треугольника АСД.
Этот треугольник - половина равностороннего треугольника, высота которого равна СД,
а сторона равна стороне АС=9
а) СД=АС* (√3):2=4,5√3
или
б) СД=АС*sin60, что одно и то же.
Радиус АО=ОД
Треугольник АОД - равнобедренный.
АД противолежит углу АСД, равному 30 градусов, и равна половине АС.
АД=9
:2=
4,5 см
Из треугольника АОД, образованного основанием АД сечения и радиусами,
найдем эти радиусы, проведя в нем высоту ОН.
Радиус ОД=НД
:sin 60
НД=АД
:2=2,25см
R=ОД=2,25
: (√3)
:2=
1,5√3 см
Длина окружности основания равна
C=2πR=
3√3см
Площадь основания равна
S=πr²=
6,75π см²
Площадь боковой поверхности
Sбок=3√3*4,5√3=
40,5 см²
Sполная=40,5+2*6,75π=40,5+13,5 π=40,6+≈42,4=≈82,9 см²