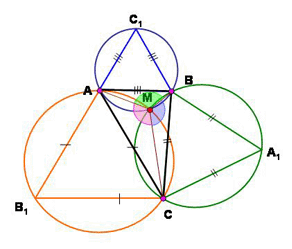
Т.к. ∠AMB=∠BMC=∠CMA=360/3=120 , то значит точка М - точка Торричелли (точка треугольника, из которой все стороны видны под углом в 120°).
1) Eсли построить на стороне BC треугольника ABC внешним образом правильный треугольник A1BC, то точка М будет лежать на окружности, описанной около треугольника A1BC (∠BMC=120, ∠BА1C=60), с радиусом R1=BC/√3=9/√3.
Эта же окружность описана и около треугольника МВС, значит можно найти его площадь Smbc=MB*MC*BC/4R1=MB*MC*√3/4.
2) точно так же строим на стороне АС равносторонний треугольник АВ1С, для него R2=AC/√3=4/√3, Smac=MA*MC*AC/4R2=MA*MC*√3/4.
3) aналогично на стороне АВ построим треугольник АС1В, для него
R3=AB/√3=6/√3, Smab=MA*MB*AB/4R3=МА*МВ*√3/4.
4) площадь треугольника АВС находим по ф.Герона
Sabc=√р(р-АВ)(р-ВС)(р-АС)=√9,5*3,5*0,5*5,5=0,25√1463, где полупериметр р=(АВ+ВС+АС)/2=(9+4+6)/2=9,5.
5) Tакже площадь Sabc=Smbc+Smac+Smab, подставим:
0,25√1463=√3/4*(MB*MC+MA*MC+MA*MB), значит
MB*MC+MA*MC+MA*MB=0,25√1463:√3/4=√1463/3.
6) Теперь применим теорему косинусов:
- для треугольника МВС
ВС²=МС²+МВ²-2МС*МВ*соs 120. cos 120=-1/2
81=МС²+МВ²+МС*МВ
- для треугольника МАС
АС²=МС²+МА²-2МС*МА*соs 120.
16=МС²+МА²+МС*МА
- для треугольника МАВ
АВ²=МА²+МВ²-2МА*МВ*соs 120.
36=МА²+МВ²+МА*МВ
7) если все 3 выражения сложить, получится
81+16+36=МС²+МВ²+МС*МВ+МС²+МА²+МС*МА+МА²+МВ²+МА*МВ
133=2(МС²+МА²+МВ²)+(МС*МВ+МС*МА+МА*МВ)
133=2(МС²+МА²+МВ²)+√1463/3
МС²+МА²+МВ²=(133-√1463/3)/2≈(133-22,08)/2=55,46≈55