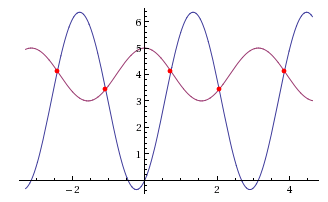
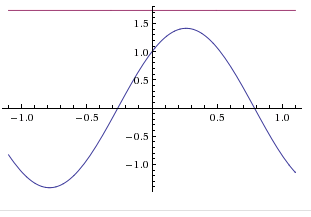
Решал графически, графики приложил к фото
1)6sin^2 x +3/2sin2x=2cos^2 x+3
x ∈ {(2*пи*k+asin(корень(877-96*корень(69))*(8*корень(69)+6)/(219*корень(69)-1168)))/2, (2*пи*k+asin((8*корень(69)-6)*корень(96*корень(69)+877)/(219*корень(69)+1168))-пи)/2}, k ∈ Z
2) sin3x+cos3x=√3
x ∈ ∅; (икс принадлежит пустому множеству, т.к. графики функций не пересекаются)