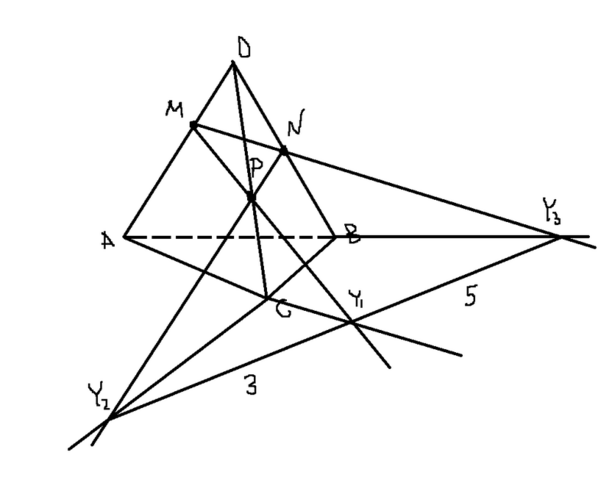
Плохо, что у тебя не даны соотношения, допустим AM:MD и т.д. Потому что в твоем случае нужно правильно расставить точки. Например, N не может быть выше, чем M, Р не может быть выше, чем М. А дальше необходимо думать о том, как поставить N и Р, я поставил Р ниже, тогда выходит правильное равенство.
Решение фактически сводится к графическому(вкладываю график). Как видно по графику, образовалась плоскость AY₃Y₂, прямая Y₂Y₃ Лежит в этой плоскости, а точка Y₁ принадлежит прямой.
⇒ Y₂Y₃=Y₁Y₂+Y₁Y₃=5+3=8 см.
Ответ: 8 см.