Найдите точки экстремума и определите промежутки возрастания-убывания функции...

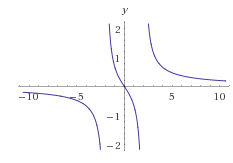
y=2x/(x^2-4)
y = (2 x)/((x-2) (x+2))

x^2-4 $\neq$ 0, y = (2 x)/(x^2-4)
x = 0, y = 0
x $\neq$ -2 x $\neq$ 2
(d)/(dx)((2 x)/(x^2-4)) = -(2 (x^2+4))/(x^2-4)^2 - это производная функции
D（y) = (-∞,-2)U(-2,2)U(2,∞)

смотри график, функция только убывает (график приложил как файл)
функция убывает на (-∞,-2)U(-2,2)U(2,∞)
~
Помог ? Ставь "спасибо" и оцени работу ! ;)