Квадрат диагонали куба равен сумме квадратов трёх его измерений ( выведена из т.Пифагора):
D²=a²+a²+a²=3а²
где
a,а,а — измерения куба, т.е., его длина, ширина и высота - они равны.
D=a√3
По условию D=3√2
Тогда
а√3=3√2
a=√3*√2=√6
Грани куба - квадраты.
Диагональ d квадрата равна его стороне, умноженной на √2 ( выводится из т.Пифагора)
d=√6*√2= 2√3
----
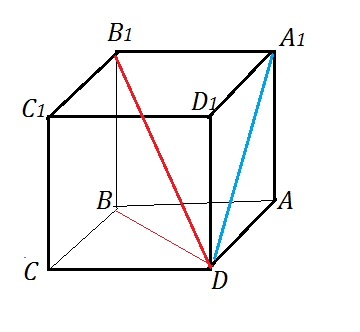
или иначе (см. рисунок)
В1D - диагональ куба,
А1D- диагональ грани.
DA1=√(B1D²-B1A1²)=√(3a²-a²)=a√2
DA1=d=√6*√2= 2√3