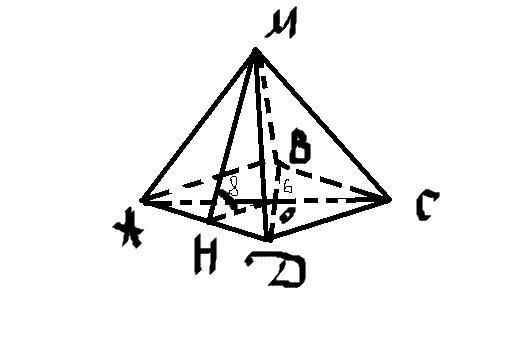
Боковая поверхность состоит из 4 одинаковых треугольников. Найдем площадь одного из них: S=1/2*AD*MH. AD - гипотенуза в прямоугольном треугольнике АОD, т.к. диагонали ромба перпендикулярны. АД=корень из 4*4+3*3=5 см.МН находим как гипотенузу из прямоугольного треугольника МОН. Синус угла МНО=5/13. Синус - отношение противолежащего катета МО к гипотенузе МН. МО/МН=5/13. По основному тригонометрическому тождеству найдем косинус этого угла корень из 1-25/169=корень из 144/169=12/13. Т.о. ОН/МН=12/13. ОН - высота в прямоугольном треугольнике АОД, ее можно найти по формуле АО*ОД/АД=4*3/5=2,4 см. 2,4/МН=12/13, отсюда МН=13/5=2,6 см. S=1/2*5*2,6=6,5 см. кв. Площадь боковой поверхности 4*6,5=26 см.кв.