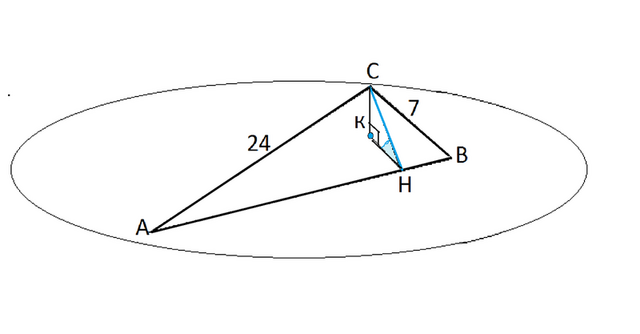
Пусть данный в условии треугольник будет АВС,
угол С=90, СВ=7 см, АС=24 см.
Треугольник имеет отношение сторон из Пифагоровых троек 7:24:25. ⇒ Гипотенуза этого треугольника равна 25 см.
(Можно проверить по т. Пифагора)
Сделаем чертеж.
Перпендикуляр СК - искомое расстояние.
СН - высота данного треугольника, НК - ее проекция на плоскость.
В прямоугольном треугольнике СКН катет СК противолежит углу 30°
, ⇒
он равен половине гипотенузы СН.
Высота прямоугольного треугольника - среднее пропорциональное произведений отрезков, на которые она делит гипотенузу.
НВ - проекция катета СВ на гипотенузу.
Катет прямоугольного треугольника - среднее пропорциональное произведения гипотенузы на проекцию этого катета. ⇒
СВ²=АВ*ВН
49=25 ВН
ВН=49:25=
1,96 см
СН²=АН*ВН= (25-1,96)*1,96=45,1584
СН= 6,72 см
СК=6,72:2=3,36 см