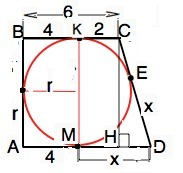
В трапеции АВСD основания ВС||AD (см. рисунок).
АВ⊥ВС и АD.
АВ=2r=8 и является высотой АВСD. Стороны трапеции - касательные к вписанной в нее окружности.
Отрезки касательных из одной точки до точек касания равны.
КС=СЕ=6-4=2 см, МD=ED=х
Опустим высоту СН=АВ=8
АН=6, МН=АН-АМ=6-4=2
В прямоугольном ∆СНD гипотенуза СD=х+2, катет HD=х-2
По т.Пифагора СD²-CD²=CH²
х²+4х+4-х²+4х-4=64
8х²=64
х=√64=8 см
AD=8+4=12 см
S=0,5•(AD+BC)•CH=0,5•(6+12)•8=72 см²