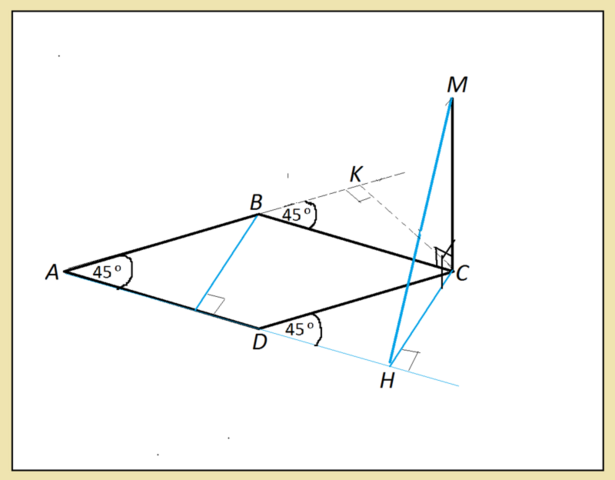
Стороны ромба содержатся в четырех прямых:
АВ, ВС, СD и АD.
Расстояние от М до ВС и СD равно МС=7 см, т.к. расстояние от точки до прямой - перпендикуляр, а по условию МС ⊥ плоскости ромба.
Расстояние от М до прямой, содержащей сторону АD, равно наклонной МН, проведенной перпендикулярно к этой прямой.
Длину ее найдем из прямоугольного треугольника МСН, в котором НС равна и параллельна высоте ромба.
Угол СDН=углу А=45°
СН=СD*sin (45°)=(8*√2):2=4√2 см
МН=√(МС+СН)=√(32+49)=9 см
Точно таким же будет расстояние до прямой, содержащей сторону АВ, т.к. все стороны ромба и соответственные углы при параллельных сторонах равны.
Ответ: 7 см до ВС и СD, и 9 см до АВ и АD
bzs*