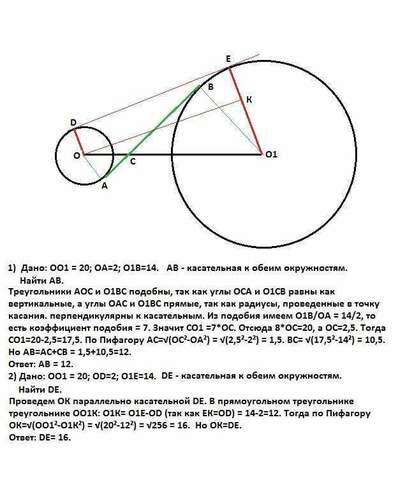
1) Дано: ОО1 = 20см; ОА=2см; О1В=14см. АВ - касательная к обеим окружностям.
Найти АВ.
Треугольники АОС и О1ВС подобны, так как углы ОСА и О1СВ равны как вертикальные, а углы ОАС и О1ВС прямые, так как радиусы, проведенные в точку касания, перпендикулярны к касательным. Из подобия имеем О1В/ОА = 14/2, то есть коэффициент подобия = 7. Значит СО1 =7*ОС. ОО1=ОС+СО1 или ОО1=ОС+7*ОС. Отсюда 8*ОС=20см, а ОС=2,5см. Тогда СО1=20-2,5=17,5см.
По Пифагору АС=√(ОС²-ОА²) = √(2,5²-2²) =1,5см. ВС= √(17,5²-14²) =10,5см.
Но АВ=АС+СВ = 1,5+10,5=12см.
Ответ: АВ = 12см.
2) Дано: ОО1 = 20см; ОD=2см; О1Е=14см. DЕ - касательная к обеим окружностям.
Найти DE.
Проведем ОК параллельно касательной DE. В прямоугольном треугольнике ОО1К: О1К= О1Е-ОD (так как ЕК=ОD) = 14-2=12см.
Тогда по Пифагору OK=√(ОО1²-О1К²) = √(20²-12²) = √25б = 16см.
Но ОК=DЕ.
Ответ: DЕ = 16см.
Ответ в приложенном рисунке.