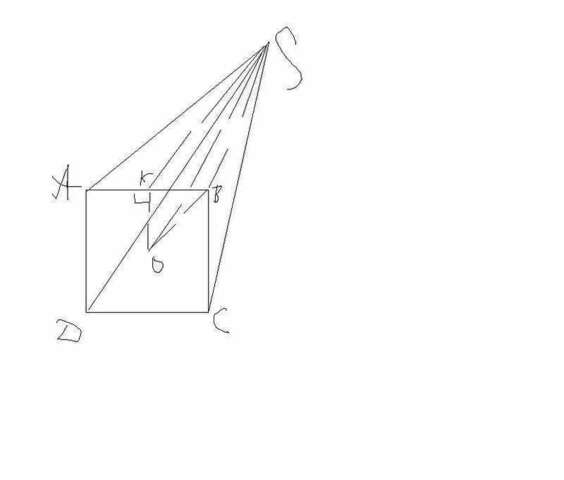
Точка, равноудаленная от вершин проєктируется в центр описанной окружности
AB=BC=CD=AD = 8 дм,
OS=9 дм
радиус вписанной окружности 
По теореме Пифагора расстояние от точки до сторон квадрата будет
см
ответ: корень(97)
Пусть первый рабочий делает х деталей в час, тогда второй делает х-4 деталей в час. по условию задачи составляем уравнение:
значит первый рабочий делает в час 12 деталей
второй рабочий в час делает 12-4=8 деталей
ответ: 8 деталей в час
0; 4-x>0;\\ xx<5; x<4;\\ x<4;\\ log_2 (5-x)+log_2 (4-x)=log_{2^{-1}} 0.05;\\ log_2 (5-x)+log_2 (4-x)=log_{2} 0.05^{-1};\\ log_2 (5-x)(4-x)=log_{2} 20;\\ (5-x)(4-x)=20;\\ 20-9x+x^2=20;\\ x^2-9x=0;\\ x(x-9)=0;\\ x_1=0; x_2=9>4" alt="log_2 (5-x)+log_2 (4-x)=log_{0.5} 0.05;\\ 5-x>0; 4-x>0;\\ xx<5; x<4;\\ x<4;\\ log_2 (5-x)+log_2 (4-x)=log_{2^{-1}} 0.05;\\ log_2 (5-x)+log_2 (4-x)=log_{2} 0.05^{-1};\\ log_2 (5-x)(4-x)=log_{2} 20;\\ (5-x)(4-x)=20;\\ 20-9x+x^2=20;\\ x^2-9x=0;\\ x(x-9)=0;\\ x_1=0; x_2=9>4" align="absmiddle" class="latex-formula">
ответ: 0
