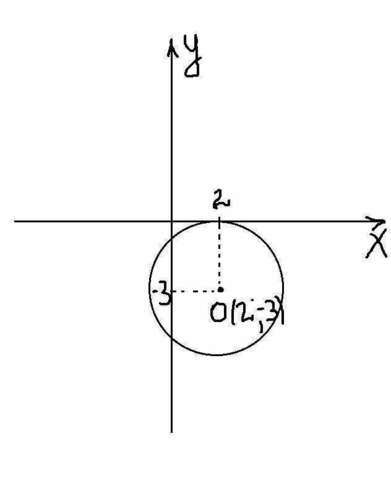
Уравнение окружности с центром в точке О(х₀; у₀) имеет вид
(x-x₀)²+(y-y₀)²=R²
По условию O(2; -3), поскольку окружность касается оси абсцисс, то расстояние от центра окружности, то точки касания с осью абсцисс равно
R=(0-(-3)=3
Подставим координаты центра окружности и радиус в уравнение окружности.
(x-2)²+(y-(-3))²=3²
(x-2)²+(y+3)²=9