Приравниваем две функции. Приводим подобные слагаемые. Выделяем x. Смотрим при каком значении p уравнение не имеет решений.
p^2x + p - 8 = 4x - 6
xp^2 + p - 8 - 4x + 6 = 0
xp^2 + p - 4x - 2 = 0
xp^2 - 4x + p - 2 = 0
x(p^2 - 4) + p - 2 = 0
x(p-2)(p+2) = 2 - p
x = (2-p)/(p - 2)(p+2)
x = - (p - 2) / ( p -2)(p + 2)
x = - 1/(p + 2)
О.Д,З
p ≠ - 2
Если p = - 2 , то
y = 4x - 2 - 8 = 4x - 10
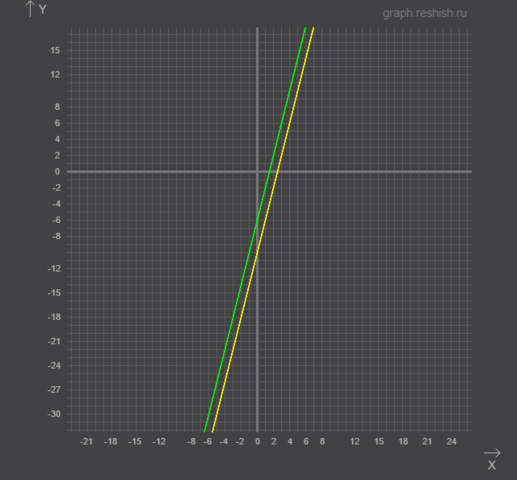
y = 4x - 6
У графиков нет точек пересечений. Внизу график.
Ответ: при р равном -2 . прямые у=р^2 * x+p-8 и y=4x-6 не имеют общих точек.