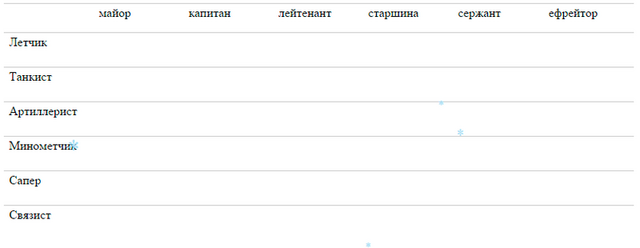
Эту задачу можно решить с помощью алгебра логики, а можно проще - с помощью таблицы.
Просто берешь и поэтапно крестиком отмечаешь пересечение, которое невозможно. Ну вот, к примеру, если в первом туре лейтенант выиграл у летчика, майор у танкиста, а сержант у минометчика, то ты ставишь себе метку в таблице на пересечении, что лейтенант не может быть летчиком, танкистом или минометчиком. Также и с остальными.
Капитан - не танкист и не минометчик. Ефрейтор - не минометчик. Майор, вдобавок к тому, что он не летчик, не танкист и не минометчик еще и не связист (т.к. в 4 туре выиграл у последнего). Поскольку хуже всех выступил сапер, то майор и лейтенант не могут быть им, ведь они победители. Следовательно майор - артиллерист. Теперь стало ясно, что остальные не могут быть артиллеристами. Идем дальше. Поскольку еще с самого начала мы знаем, что лейтенант не может быть минометчиком, летчиком и танкистом, а теперь еще и артиллеристом (т.к. майор - артиллерист) и сапером, то остается только связист. Значит, лейтенант - связист. Из этого следует, что сержант - сапер. Теперь расставим остальные пересечения и получим:
Майор - артиллерист
Лейтенант - связист
Сержант - сапер
Старшина - минометчик
Капитан - летчик
Ефрейтор - танкист