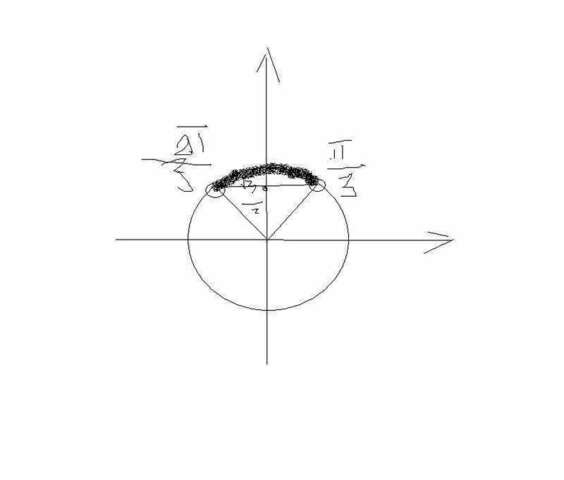
0;\\ sin 3x+sin 3x-\sqrt{3}>0;\\ 2sin 3x-\sqrt{3}>0;\\ sin (3x)>\frac{\sqrt{3}}{2};\\ \frac{\pi}{3}+2* \pi*k < 3x< \frac{2 \pi}{3}+2*\pi*k;\\ \frac{\pi}{9}+\frac{2* \pi*k}{3}0;\\ sin 3x+sin 3x-\sqrt{3}>0;\\ 2sin 3x-\sqrt{3}>0;\\ sin (3x)>\frac{\sqrt{3}}{2};\\ \frac{\pi}{3}+2* \pi*k < 3x< \frac{2 \pi}{3}+2*\pi*k;\\ \frac{\pi}{9}+\frac{2* \pi*k}{3}
0;\\ sin 3x+sin 3x-\sqrt{3}>0;\\ 2sin 3x-\sqrt{3}>0;\\ sin (3x)>\frac{\sqrt{3}}{2};\\ \frac{\pi}{3}+2* \pi*k < 3x< \frac{2 \pi}{3}+2*\pi*k;\\ \frac{\pi}{9}+\frac{2* \pi*k}{3}0;\\ sin 3x+sin 3x-\sqrt{3}>0;\\ 2sin 3x-\sqrt{3}>0;\\ sin (3x)>\frac{\sqrt{3}}{2};\\ \frac{\pi}{3}+2* \pi*k < 3x< \frac{2 \pi}{3}+2*\pi*k;\\ \frac{\pi}{9}+\frac{2* \pi*k}{3}
ответ: x є