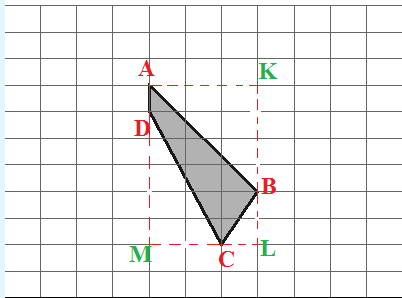
Для начала обозначим углы четырёхугольника буквами A, B, C и D, как изображено на прилагающейся картинке. Далее, беря во внимание, что сторона клетки равна 1 см, рассчитываем каждую сторону фигуры:
1) AD, как мы видим на картинке, равна 1 см(т.к сторона клетки = 1 см);
2) Сторону AD рассчитываем по теореме Пифагора(сумма квадратов катетов равна квадрату гипотенузы). Для этого проводим две вспомогательные линии к точке K( на прилагающемся рисунке это линии AK и BK), которые будут выступать у нас в роли катетов, и узнаём размерности каждой из них: AK = 3 см, BK = 4 см. Таким образом,  ,
,  см.
см.
3) Сторону BC узнаём аналогично предыдущей стороне: проводим два катета BL и CL(всё изображено на рисунке), узнаём их размерности: BL = 2 см, CL = 1 см, и по этой же теореме узнаём BC:  см.
см.
4) Всё по той же схеме узнаём CD(процесс писать не буду, ибо надеюсь, что принцип понятен).  см.
см.
Далее, для нахождения площади используем следующую формулу:  . Но сначала найдём p - полупериметр. p в данном случае равняется
. Но сначала найдём p - полупериметр. p в данном случае равняется  ≈ 6,8 см.
≈ 6,8 см.

 ≈ 8,2 см²
≈ 8,2 см²
P.S. Все размерности я округлял, как, например,  или
или , исключительно для удобства расчёта.
, исключительно для удобства расчёта.