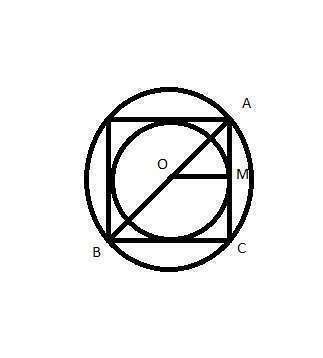
Диаметр описанной окружности равен 12 см, следовательно диагональ квадрата равна АВ=12 см.
Треуг АВС - прямоуг. и равнобедр. По т. Пифагора:
АВ²=2АС² => AC=AB/√2=12/√2
В треуг. АВС: ОМ - сред. лин. (АО=ОВ как радиусы опис. окр., АМ=МС, тк. ОМ - радиус впис. окр.). Значит ОМ = 1/2*ВС = 6/√2 - радиус опис. окр
Длина впис окр = 6П√2