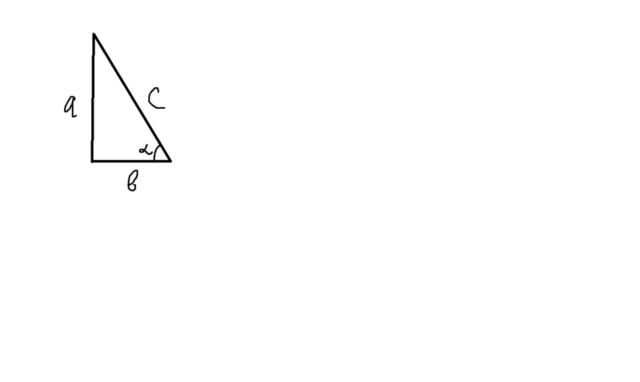применим метод прямоугольного треугольника. Сейчас я опишу его действие. Он позволяет вычислять точныее значения нетабличных углов. Построим прямоугольный треугольник. Пусть у нас угол α будет при стороне b. Пусть arccos 2/3 = α, тогда по определению арккосинуса cos α = 2/3. Видно, что нам надо найти tg 2α. Применим формулу тангенса двойного угла:
tg 2α = 2tg α / 1 - tg² a.
Отсюда следует, что нам нужно найти tga. tg α = sin α/cosα. Косинус мы знаем, надо найти синус.
cos α = b / c
b / c = 2/3
b = 2, c = 3
sin α = a / c
a = √(c² - b²) = √5
Отсюда sin α = √5 / 3
tg α = sin α / cosα = √5/3 : 2/3 = √5/2
Теперь осталось найти всего лишь tg 2α:
tg 2α = √5 / 1 - 5/4 = √5 : -1/4 = -4√5
Таким образом, tg 2α = tg(2arccos 2/3) = -4√5
Ответ получен. Всё остальное делаем по аналогии. Рисунок сейчас приложу моих рассуждений