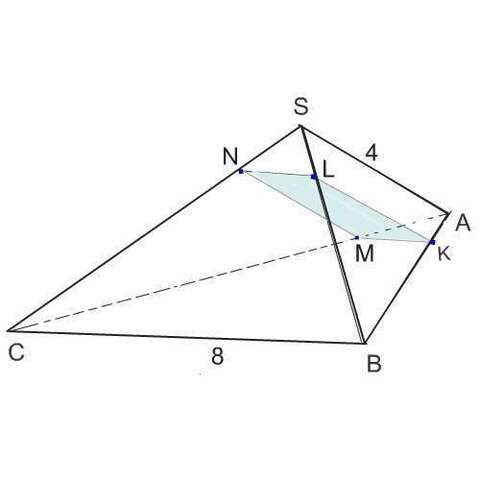
Нарисуем пирамиду, проведем в ней сечение KLNM.
Рассмотрим треугольники ВАС и КАМ.
Они подобны, т.к. МК параллельна СВ, углы в них равны- один общий А, другие по свойству углов при пересечении параллельных прямых секущей.
АК:КВ=1:3
Отсюда АВ:АК=4:1
СВ:КМ=4:1
МК=8:4=2 см
NL=MK=2 cм
Рассмотрим треугольники SBA и KBL
Они также подобны: в них равны- один общий угол В, другие по свойству углов при пересечении параллельных прямых секущей.
АВ:АК=3:1 по условию задачи
ВК:АВ=3:4
KL:AS=3:4
KL:4=3:4
KL=NM= 3 см
Периметр сечения равен
Р=2(3+2)=10 см