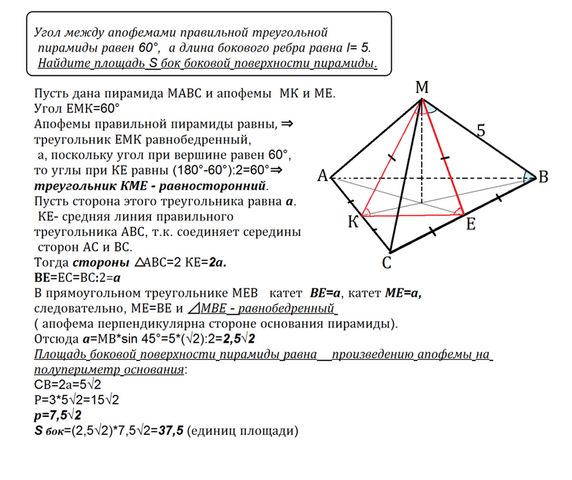
Угол между апофемами правильной треугольной пирамиды равен 60°, а длина бокового ребра равна l= 5. Найдите площадь S бок боковой поверхности пирамиды.
Пусть дана пирамида
МАВС, её апофемы
МК и
МЕ.
Угол ЕМК=60°
Апофемы правильной пирамиды равны. ⇒
треугольник ЕМК равнобедренный, а, поскольку угол при вершине равен 60°, то углы при КЕ равны (180°-60°):2=60°⇒
треугольник КМЕ - равносторонний.
Пусть сторона этого треугольника равна
а.
КЕ- средняя линия правильного треугольника АВС, т.к. соединяет середины сторон АС и ВС.
Тогда стороны △АВС=2 КЕ=2а.
ВЕ=ЕС=а
В прямоугольном треугольнике МЕВ катет ВЕ=а, катет МЕ=а, следовательно, МЕ=ВЕ и ⊿ МВЕ - равнобедренный
( апофема перпендикулярна стороне основания пирамиды).
Отсюда а=МВ*sin 45°=5*(√2):2=2,5√2
Площадь боковой поверхности пирамиды равна произведению апофемы на полупериметр основания:
CВ=2а=5√2
Р=3*5√2=15√2
р=7,5√2
S=(2,5√2)*7,5√2=37,5 (единиц площади)