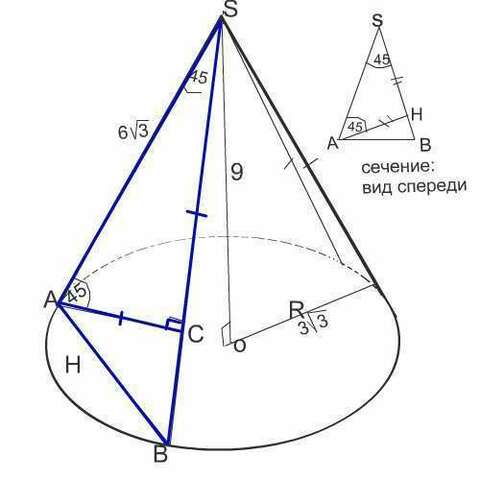
Так как угол при вершине осевого сечения равен 60°, то осевое сечение представляет собой равносторонний треугольник, углы при основании в нем тоже 60°. .
Дана его высота=9, отсюда нетрудно вычислить образующую SA конуса. Она равна стороне равностороннего треугольника.
sin 60°√3:2.
h:SA= √3:2
2h=SA√3
SA=18:√3=6√3 - это образующая конуса.
Сечение конуса, площадь которого необходимо найти, является равнобедренным треугольником с углом при вершине 45° и боковыми сторонами, равными образующей конуса и равными 6√3.
Площадь треугольника равна половине произведения высоты на основание.
Основание известно - это образующая. Проведем к нему высоту АС и получим равнобедренный прямоугольный треугольник АСS, в котором высотаАС=SC.
Так как гипотенуза AS этого треугольника известна, найдем высоту h=АС=SC
АС:AS =sin 45 =(√2):2
АС=(АS* √2):2
АС=(6√3*√2):2
АС=(6√6):2=3√6
АС=3√6 -высота плоскости сечения, проведенная к SB.
S сечения=3√6*6√3:2=3√6*3√3 =9√18=27√3 см²