Из точки A, находящейся вне окружности с центром O, проведены две касательные AB и AC (B...

Question

Из точки A, находящейся вне окружности с центром O, проведены две
касательные AB и AC (B и C — точки касания). Отрезок AO пересекается с
окружностью в точке D и с отрезком BC в точке F . Прямая BD пересекает отрезок AC в
точке E. Известно, что площадь четырёхугольника DECF равна площади треугольника
ABD. Найдите угол OCB.

Answer 1

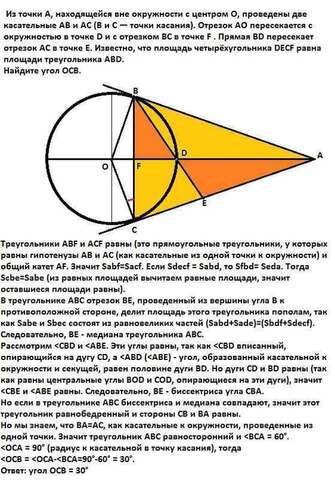
Треугольники АВF и АСF равны (это прямоугольные треугольники, у которых равны
гипотенузы АВ и АС (как касательные из одной точки к окружности) и общий катет АF. Значит Sabf=Sacf. Если Sdecf = Sabd, то Sfbd= Seda. Тогда Scbe=Sabe (из равных площадей вычитаем равные площади, значит оставшиеся площади равны).
В треугольнике АВС отрезок ВЕ, проведенный из вершины угла В к противоположной стороне, делит площадь этого треугольника пополам, так как Sabe и Sbec состоят из равновеликих частей (Sabd+Sade)=(Sbdf+Sdecf).
Следовательно, ВЕ - медиана треугольника АВС.
Рассмотрим дугу СD, а равен половине дуги ВD. Но дуги CD и BD равны (так как равны центральные углы ВОD
и СОD, опирающиеся на эти дуги), значит  Следовательно, ВЕ - биссектриса угла СВА.
Но если в треугольнике АВС биссектриса и медиана совпадают, значит этот треугольник равнобедренный и стороны СВ и ВА равны.
Но мы знаем, что ВА=АС, как касательные к окружности, проведенные из одной точки. Значит треугольник АВС равносторонний и <ВСА = 60°. <br>Ответ: угол ОСВ = 30°

---