Точки дотику вписаного у прямокутну трапецію кола ділять більшу сторону на відрізки 9 і...

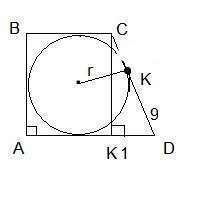
Відстань від центра кола до бічної сторони - радіус вписанного кола, тобто r.
r=√(СK*CD)=√(9*16)=3*4=12
За властивістю вписанного кола в трапецію
сума основ=сумі бічних сторін
AD+BC=AB+CD; AD+BC=12+25; AD+BC=37
З трикутника CKK₁(угол CK₁K=90°)
CK₁=2r=24; CD=25;
K₁D=√(25²-24²)=7

ВС+(АК₁+К₁Д)=37
ВС+ВС+7=37
2ВС=30
ВС=15

АД=15+7=22

Периметр трапеції: P=25+24+22+15=86

Ответ: 86.

Точки дотику вписаного у прямокутну трапецію кола ділять більшу сторону ** відрізки 9 і...