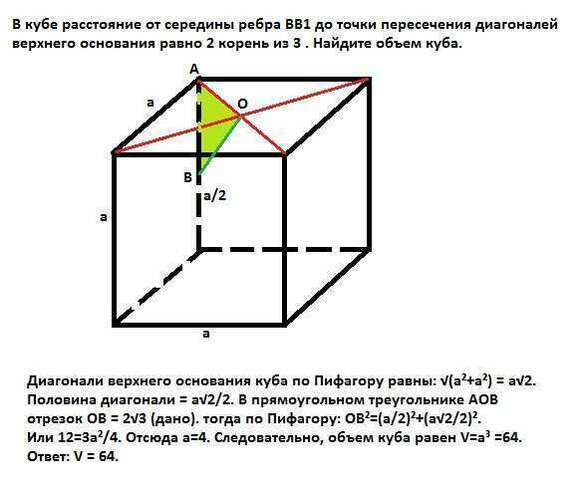
Диагонали граней куба равны а√2, где а - ребро куба. Значит половина диагонали равна а√2/2. В прямоугольном треугольнике АОВ отрезок ОВ=2√3 (дано). Тогда по Пифагору ОВ²=АВ²+АО² = (а/2)²+(а√2/2)². Подставив известные величины, имеем:
12=3а²/4, отсюда а=4, а объем куба = а³ = 64.
Ответ:V = 64.