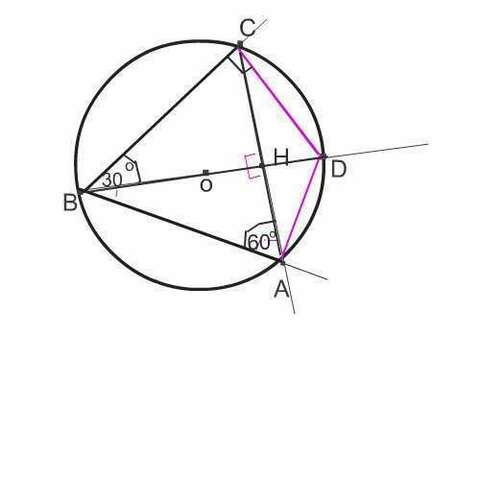
Соединим точки А,В и С в треугольник.
Каждый угол этого треугольника опирается на равную дугу. Так как углы вписанные, то они равны ½ ·360:3=60°.
Соединим последовательно точки С, D, А. Получившийся четырехугольник АВСD - вписанный. Сумма противоположных углов вписанного четырехугольника равна 180°
∠ СВА+ ∠СDА=180°.
∠СDА =180-60=120°
ВD - биссектриса ∠ В по условию задачи.
Поскольку Δ АВС - равносторонний, биссектриса в нем и высота, и медиана. Отсюда СА⊥ВD, СН=АН.
Δ ВСD=Δ ВАD по первому признаку равенства треугольников:
в них равны стороны АВ и ВС, сторона ВD общая, равен и угол между этими сторонами.
∠СВD=60:2=30°
∠ СDВ=120:2=60°
∠ ВСD=180- (60+30)=90°
Δ СВD - прямоугольный.
ВD - его гипотенуза.
Гипотенуза вписанного прямоугольного треугольника является диаметром окружности, в которую этот треугольник вписан.
ВD- диаметр, что и требовалось доказать.