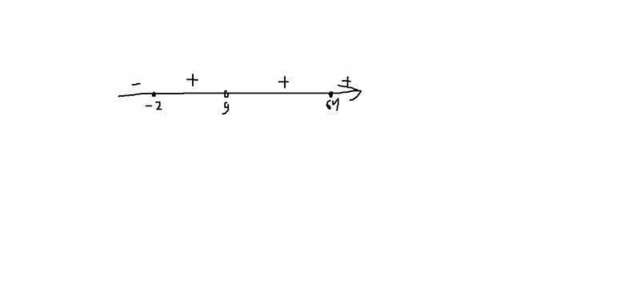
5. в) Здесь всё уже разбито на множители, поэтому осталось только нанести нули и не имеющие смысла выражения на прямую и верно поставить знаки. рисунок первого решения сейчас приложу. Отсюда выписываем те интервалы, где значение выражения меньше или равны 0. Это (-∞;-2] ∨ {64}
6.a) У нас выражение - дробь. А дробь имеет смысл, если его знаменатель не равен 0. С другой стороны - в знаменателе у нас стоит квадратный корень, который имеет смысл, если его подкоренное выражение неотрицательно. Отсюда естественно вытекает, что подкоренное выражение должно быть только больше нуля. составим и решим неравенство:
(4 - x)(x + 6) >0
Вынесем минус за скобки в левой части и домножим всё на -1:
-(x - 4)(x + 6) > 0
(x - 4)(x + 6) <0</p>
Теперь в действие вступает стандартный метод интервалов. Получаем в результате интервал:
(-6;4)
Это и будет областью определения функции.
7)Чтобы решить систему неравенств, необходимо сначала решить по-отдельности каждое неравенство, а затем найти объединение полученных промежутков. Решим первое неравенство:
x² - x - 2 > 0
(x - 2)(x + 1) > 0
Решая методом интервалов, получим:
(-∞;-1) ∨ (2;+∞)
Решаем второе неравенство:
10x + 25 > 0
10x > -25
x > -2.5
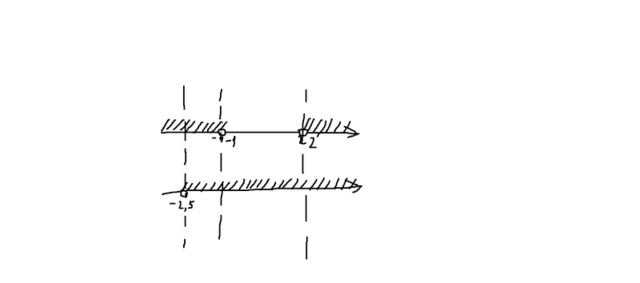
Теперь приведу рисунок, на котором найду окончательное решение всей системы. на рисунке решения каждого неравенства показаны штриховкой, решением системы соответственно будут участки, где штриховки совпадают, я их и нашёл. Это:
(-2.5;-1) ∨ (2;+∞) - решение системы.
10)а) Следует помнить, что решение неравенств высших порядков(степени, выше первой) должно осуществляться с помощью метода интервалов. Для этого, условие номер 1 - разложить исходное выражение на множители. Этим и займёмся. Разложим на множители левую часть неравенства:
16x³ - 32x² - x + 2 = (16x³ - 32x²) - (x - 2) = 16x²(x - 2) - (x-2) = (x-2)(16x² - 1) = (x-2)(4x-1)(4x+1)
Неравенство примет вид:
(x-2)(4x - 1)(4x+1) <0</p>
Теперь решаем обычным методом интервалов, посколько коэффициенты при x уже положительны. Решая, получаем следующий промежуток:
(-∞;-1/4) ∨ (1/4;2) - это решение данного неравенства.