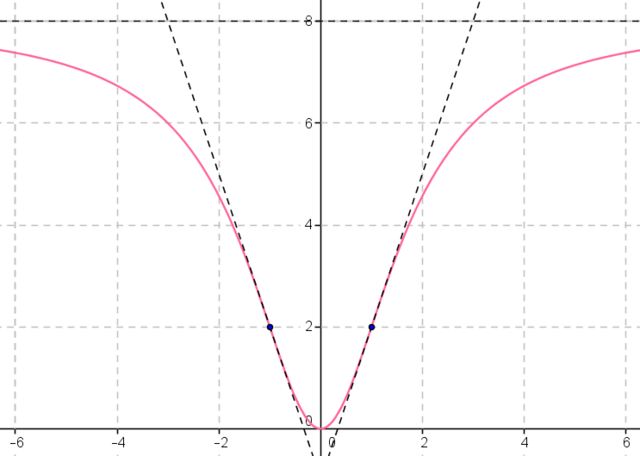
Y = 8x^2 / (x^2 + 3) = 8(x^2 + 3 - 3) / (x^2 + 3) = 8 - 24 / (x^2 + 3)
- D[y] = R
- точек разрыва нет
- y = 0 <-> x = 0, пересекает оси в начале координат.
- четная
- убывает на (-infty, 0], возрастает на [0, infty)
Объяснение: очевидно из вида 8 - 24 / (x^2 + 3) - при увеличении x по модулю второе слагаемое убывает, а сумма растет.
- минимум при x = 0, максимума нет (асимптотически 8 на бесконечностях) [из прошлого пункта]
- y' = -(24 / (x^2 + 3))' = 24 / (x^2 + 3)^2 * 2x = 48x / (x^2 + 3)^2
y'' = 48 / (x^2 + 3)^2 - 96x / (x^2 + 3)^3 * 2x = 48((x^2 + 3) - 4x^2) / (x^2 + 3)^3 = 144(1 - x^2) / (x^2 + 3)^3
-1 <= x <= 1: y'' > 0, выпуклая
(-infty, -1], [1, infty): y'' < 0, вогнутая
+-1 - точки перегиба.
- вертикальных асимпот нет
- горизонтальная асимптота y = 8