Точка М расположена ** стороне СD квадрата АВСD с центром О, причем СМ:МD=1:2. Найдите...

Question

Точка М расположена на стороне СD квадрата АВСD с центром О, причем СМ:МD=1:2. Найдите стороны треугольника АОМ, если сторона квадрата равна 6. Решать без тригонометрии. Теорему Пифагора использовать можно

Comments

AO половина диагонали АС, которая равна кореньиз (36+36)=6*кореньиздвух, тогда АО равна 3*кореньиздвух

---

СМ=2, МD=4, тогда по теореме Пифагора АМ= кореньиз (36+16)=2*кореньиз (13)

---

ОМ найдем по теореме косинусов

---

ОМ^2=ОС^2+СМ^2-2*ОС*СМ*cos(45)

---

без косинусов решить надо

---

первые 2 стороны Вы нашли. Осталась еще одна

Answer 1

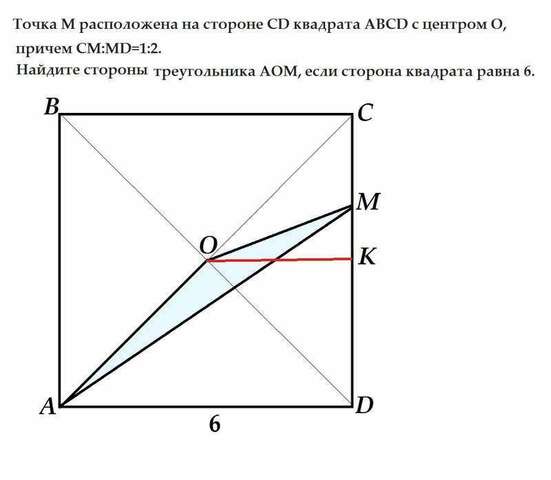
Сторона квадрата равна по условию 6. 
Т.к. СМ:МD=1:2, СМ равна одной трети стороны СD и равна 6:3=2, 
а МД=2/3 стороны СD и равна 6:3*2=4
По т. Пифагора АМ²=АD²+МD²=36+16=52
52=4*13
АМ=√(4*13)=2√13
АО - половина диагонали данного квадрата.
Диагональ квадрата находим по формуле d=a√2
АО=6√2):2=3√2
Проведем из О к середине СD прямую ОК параллельно АD. 
ОК-средняя линия треугольника АСD.
ОК=6:2=3
СК=СD:2=3
МК=СК-СМ=3-2=1
По т. Пифагора ОМ=√(ОК² +КМ² )=√(9+1)=√10
Стороны треугольника АОМ:
АМ=2√13
АО=3√2
ОМ=√10

---

Comments

Cпасибо

---

я понял

Answer 2

Опустим перпендикуляр ON на сторону CD.
CN=ON=3 - половине стороны квадрата
MN=CN-CM=3-2=1
MD=CD-CM=6-2=4
1) OM^2=ON^2+MN^2=9+1=10;
OM=√10
2) AM^2=AD^2+DM^2=36+16=52
AM=√52=2√13
3) AO=1/2*AC; AC=AD√2
AO=1/2*6√2=3√2

Comments

спасибо