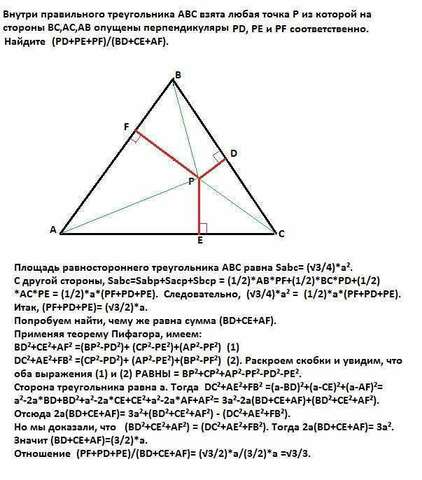
Площадь равностороннего треугольника АВС равна Sabc= (√3/4)*а².
С другой стороны, Sabc=Sabp+Sacp+Sbcp = (1/2)*AB*PF+(1/2)*BC*PD+(1/2)*AC*PE = (1/2)*a*(PF+PD+PE). Следовательно,
(√3/4)*а² = (1/2)*a*(PF+PD+PE).
Итак, (PF+PD+PE)= (√3/2)*а.
Попробуем найти, чему же равна сумма (BD+CE+AF).
Применяя теорему Пифагора, имеем:
BD²+CE²+AF² =(BP²-PD²)+ (СP²-PE²)+(AP²-PF²) (1)
DC²+AE²+FB² =(CP²-PD²)+ (AP²-PE²)+(BP²-PF²) (2).
Раскроем скобки и увидим, что оба выражения (1) и (2) РАВНЫ
(равны значению: BP²+СP²+AP²-PF²-PD²-PE²).
Сторона треугольника равна а. Тогда DC²+AE²+FB² =(а-BD)²+(а-CE)²+(а-AF)²=
a²-2a*BD+BD²+a²-2a*CE+CE²+a²-2a*AF+AF²=
3a²-2a(BD+CE+AF)+(BD²+CE²+AF²).
Отсюда 2a*(BD+CE+AF) = 3a²+(BD²+CE²+AF²) - (DC²+AE²+FB²).
Но выше мы доказали, что (BD²+CE²+AF²) = (DC²+AE²+FB²). Тогда 2a(BD+CE+AF)= 3a².
Значит (BD+CE+AF)=(3/2)*а. (или равно полупериметру треугольника (3*а)/2).
Отношение (PF+PD+PE)/(BD+CE+AF)= (√3/2)*а/(3/2)*а =√3/3.