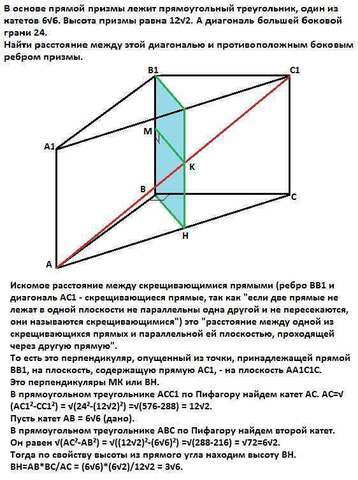
Искомое расстояние между скрещивающимися прямыми (ребро ВВ1 и диагональ АС1 - скрещивающиеся прямые, так как "если две
прямые не лежат в одной плоскости не параллельны одна другой
и не пересекаются, они называются скрещивающимися") это
"расстояние между одной из скрещивающихся прямых и
параллельной ей плоскостью, проходящей через другую прямую".
То есть это перпендикуляр, опущенный из точки, принадлежащей прямой ВВ1, на плоскость, содержащую прямую АС1, - на плоскость АА1С1С. Это перпендикуляры МК или ВН.
В прямоугольном треугольнике АСС1 по Пифагору найдем катет АС. АС=√(АС1²-СС1²) = √(24²-(12√2)²) =√(576-288) = 12√2.
Пусть катет АВ = 6√6 (дано).
В прямоугольном треугольнике АВС по Пифагору найдем второй катет.
Он равен √(АС²-АВ²) = √((12√2)²-(6√6)²) =√(288-216) = √72=6√2.
Тогда по свойству высоты из прямого угла находим высоту ВН.
ВН=АВ*ВС/АС = (6√6)*(6√2)/12√2 = 3√6.
Ответ: расстояние между диагональю АС1 и противоположным боковым ребром ВВ1 призмы равно 3√6.